반응형
Topic 2 (PART 2)
Learning Unknown Target Function
- Learning Unknown Target Function: Introduction
- 제한된 데이터셋에서 타깃 함수를 찾아낼 수 있을까?
- Learning the target function
- Inference outside training data
- 학습과정에서 학습 결과를 신뢰할 수 있을까?
- 학습되지 않은 새로운 데이터에서도 결과를 잘 도출할 수 있어야 feasible
- 그래서 다른 해결 방법이 없느냐? =>
deterministic, Rescue Plan: probabilityA 'bin' experiment - 항아리가 모집단, 항아리에서 샘플을 추출해서 mu hat을 구하여 통계적인 method를 이용한 모집단의 mu를 추정하기.
- 어떻게 mu hat과 mu를 연관 지을까?
- Hoeffding inequlity: 나쁜 이벤트의 확률이 어퍼 바운딩된다. 샘플 사이즈가 커지면 mu hat과 mu가 거의 같아진다.
- N을 키울수록, bad event가 일어날 확률이 지수적으로 감소한다. 매우 빨리 감소!
mu hat = mu: 아마도(Probably) 근사적(Approximately)으로 Correct 한 Learning => Machine Learning- 오차 범위 입실론을 아주 작게 해서 정확도를 높여야 함 => N(샘플 사이즈)를 키우자.
- Hoeffding inequlity: 나쁜 이벤트의 확률이 어퍼 바운딩된다. 샘플 사이즈가 커지면 mu hat과 mu가 거의 같아진다.
Connection to Learning
bin 모델과 learning을 어떻게 연관 지을까?
- bin 모델에선 그저 mu 값만 구하면 되었다.
- 하지만 learning에서는 X->Y로의 전체 함수 f를 알아내야 함.
- mu = error rate a hypothesis makes when approximating f
- 명확하게 연관 지을 수 있는 것
- 항아리 안의 구슬 = 하나의 데이터
- 항아리 = input space(데이터 집합, 공간)
- 샘플 = 트레이닝 데이터
- 덜 명확한 것
- Bin Coloring = hypothesis h (초록색 공이 가설이 맞았을 때, 빨간색 공 가설이 틀렸을 때)
- mu = error rate
- mu hat은 error rate의 추정치이고 unknown target function에 대해 무엇인가 말해준다.
- different h
- 가설에 따라 mu(error rate)가 달라지고, 가장 좋은 hypothesis를 골라야 한다.
Generalizing the Hoeffding Bound
- 어떻게 mu(:=error rate)를 0에 가깝게 만들까?
- 여러 hypothesis 중 best를 골라내야 함. 가설마다 mu hat도 다르고 mu 추정치도 다르다!
- mu hat is in-sample error donoted by E_in(h)
- mu is our of sample error denoted by E_out(h)
P [|E_in(h) - E_out(h)| > epsilon] <= upper bound(2e^(-2(epsilon^2) N)
BAD 이벤트가 일어날 확률이 아주 작은 값으로 upper bounding 된다!
In-Sample Error E_in(h)
- Hoeffding inequaility가 mu에서 이젠 E_in과 E_out의 관계로!
- error rate는 뽑은 샘플에 따라 달라진다.
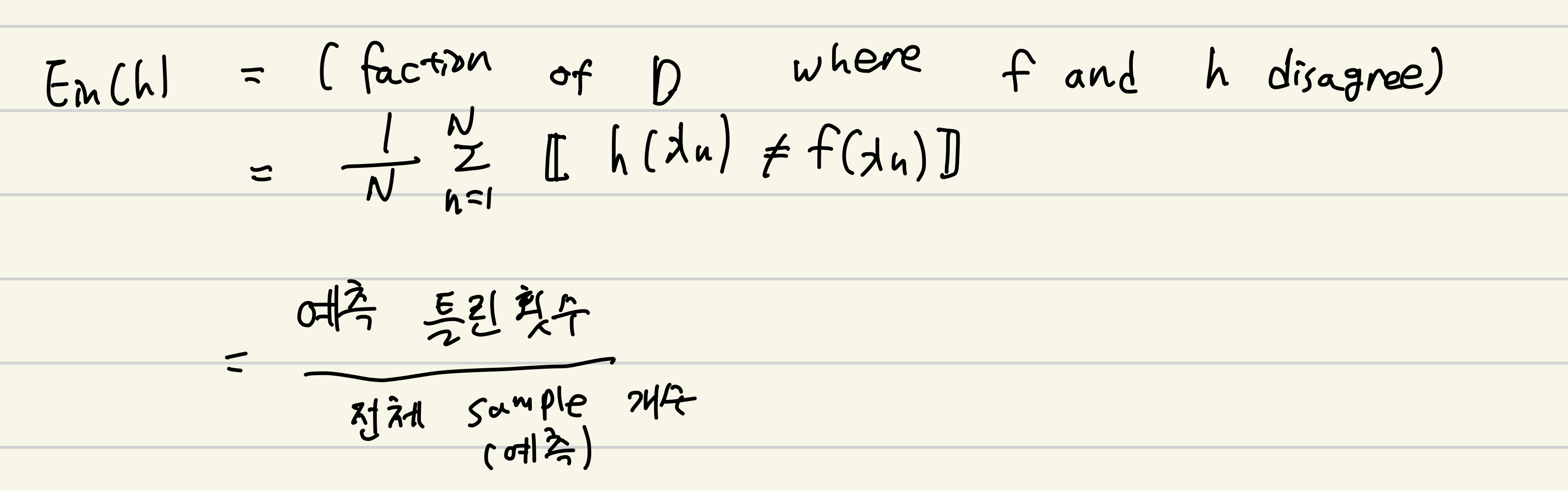
- 예측 틀린 횟수 / 전체 예측 횟수
- random variable

Out-of-Samle Error E_out(h)
- E_out(h)

Uniform version of Hoeffding inequality
- 호에프딩 부등식은 여러 개의 bin, 즉, 여러 개의 hypothesis에 동시에 적용 불가.
- 개별적인 적용은 가능
- 간단한 (but, crude 한) 해결책
- union bound 이용
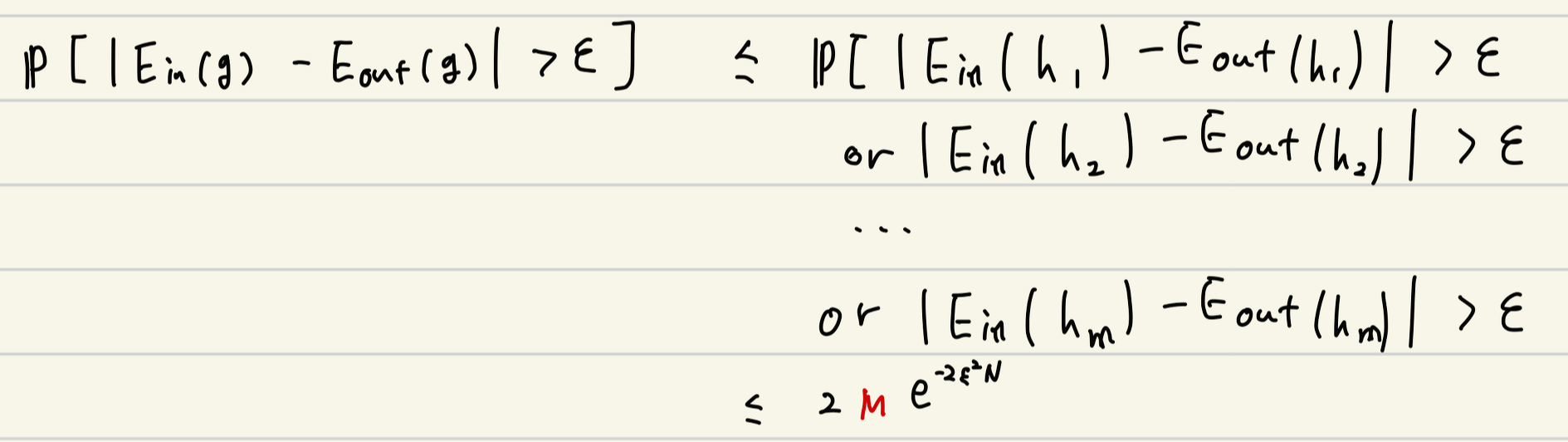
- Upper bound가 너무 커져서 별로임 -> 추정에 대한 불확실성 커진다. M배만큼 느슨해진다.
- M이 유한한 경우에만 Hoeffding inequality를 적용 가능.
반응형
'Machine Learning > AI' 카테고리의 다른 글
| [AI] 허깅페이스 디퓨저 개발을 위한 우분투와 CUDA 환경 설치 (0) | 2023.12.29 |
|---|---|
| [ML] Feasibility of Learning (0) | 2021.12.28 |
| [ML] 기계학습 기초(2021) (SNU Machine Learning Fundamentals & Applications) (0) | 2021.12.28 |
